Optimisation des shadow volumes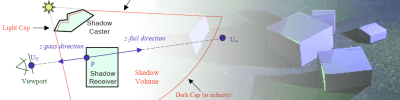

Date de publication : 15/06/2006 , Date de mise à jour : 15/06/2006

Les volumes d'ombre (shadow volumes) sont une technique assez efficace pour générer des ombres dans une scène 3D en temps réel, mais peuvent très rapidement devenir très coûteux. Ce tutoriel n'est pas l'un des 50 documents qui expliquent la technique, nous verrons plutôt ici comment mettre en oeuvre toutes sortes d'optimisations afin de tirer le meilleur de notre rendu d'ombre.

1. Introduction
2. Construction de la liste d'arêtes
3. L'algorithme multi-passes
4. Utilisation intelligente du ZFail et du ZPass
5. Extruder à l'infini
6. Extruder avec un vertex shader
7. Le double-sided stencil buffer
8. Le scissor test
9. Culling des volumes d'ombre
10. Utilisation de modèles simplifiés
11. Pour aller encore plus loin...
12. Conclusion
13. Références
14. Téléchargements

1. Introduction

La technique des volumes d'ombre est l'une des plus utilisée dans les applications 3D temps réel, et notamment les jeux vidéo. Inventée en 1977, elle s'est depuis quelques années démocratisée, depuis que les cartes graphiques permettent de l'exploiter en temps réel.

Le but de ce tutoriel n'étant pas d'expliquer une N-ième fois comment fonctionne l'algorithme, si celui-ci ne vous est pas familier vous pourrez l'étudier à l'aide la multitude de très bons documents suivants :

Practical and robust shadow volumes, nVidia
Fast, practical, and robust shadow volumes, nVidia
The Theory of real-time shadow volumes, Hun Yen Kwoon
The Mechanics of robust stencil shadows, Eric Lengyel
Real-Time shadow casting using shadow volumes, Jason Bestimt et Bryant Freitag
Définition Wikipedia, qui recense d'ailleurs la plupart des articles ci-dessus

Nous allons ici aller plus loin que la plupart de tous ces articles, et faire un état plus ou moins complet de toutes les techniques qu'il est possible d'appliquer à l'heure actuelle pour optimiser le rendu des volumes d'ombre. Une démo interactive illustrant toutes ces techniques est disponible en fin d'article, code source C++ / DirectX inclus.

2. Construction de la liste d'arêtes

Afin de construire le volumes d'ombre d'un modèle à un instant donné par rapport à une source lumineuse, il faut disposer d'une liste des arêtes du modèle. Cette liste peut être très longue à calculer, c'est pourquoi avant d'attaquer l'optimisation du rendu, nous allons nous pencher sur le moyen d'accélérer la construction d'une telle liste.

Pour rappel, voici l'algorithme basique de construction de la liste d'arêtes :

Vider ListeAretes
POUR chaque triangle T du modèle FAIRE
    POUR chacune des 3 arêtes A du triangle T FAIRE
        SI A dans ListeAretes ALORS
            Faire pointer le second triangle de A vers T
        SINON
            Ajouter A à ListeAretes
            Faire pointer le premier triangle de A vers T
        FIN SI
    FIN POUR
FIN POUR

Ce qui coûte cher dans cette étape est le fait que pour une arête (x, y) donnée, on doive rechercher si son "opposée" (y, x) n'a pas déjà été identifiée ; ce qui implique un parcours de notre liste d'arêtes pour chaque arête, soit un temps de recherche en O(N²). En gros, si vous avez 10 000 arêtes, vous allez faire 100 000 000 tours de boucles. Avec ça vous ne pourrez par exemple pas exécuter votre programme en mode debug, même pas en rêve.

Il existe des algorithmes qui s'exécutent en temps linéaire O(N) (soit 10 000 tours de boucle pour 10 000 arêtes), ce qui est très rapide, mais limité aux modèles que l'on appelle "2-manifold", c'est-à-dire dont les arêtes sont toutes partagées par deux triangles.
Un tel algorithme peut être trouvé par exemple ici :

Quickly building an edge list for an arbitrary mesh, par Eric Lengyel.

En fait, l'algorithme naïf n'a pas besoin de beaucoup pour être performant : il suffit d'avoir une structure de donnée qui soit plus adaptée qu'un simple tableau pour les recherches. On peut imaginer utiliser une table associative (std::map dans la bibliothèque standard du C++), qui donnera un algorithme en O(N log(N)), soit environ 130 000 tours de boucle pour 10 000 arêtes, ce qui est très honorable. Si vous possédez dans votre sac à dos une table de hachage, vous pourrez l'utiliser à la place de la table associative, et revenir à un temps plus proche de O(N).

Afin d'être efficaces, ces structures de données utilisent des clés de recherche. Une telle clé peut être générée très facilement pour nos arêtes : par exemple, en prenant la concaténation des indices 16 bits de ses deux sommets.

unsigned long Id = (std::min(Arete.V0, Arete.V1) << 16) | std::max(Arete.V0, Arete.V1);

Ici nous prenons bien soin de placer les indices des sommets de l'arête toujours dans le même ordre (le plus petit suivi du plus grand), afin que les couples (x, y) et (y, x), qui représentent la même arête, aient bien la même clé.

3. L'algorithme multi-passes

L'un des aspects qui est peu abordé dans les tutoriels (car non directement en rapport), est le rendu des zones d'ombre. Construire les volumes d'ombre c'est bien, déterminer quels pixels sont ombrés c'est très cool, mais ensuite ? Comment concrétiser ça à l'écran ?
A l'époque où les cartes graphiques n'étaient pas très puissantes, la technique la plus utilisée était l'affichage d'un bête rectangle recouvrant l'écran, et assombrissant (à l'aide d'alpha-blending) les pixels étant marqués "ombrés" par l'algorithme. C'est simple, pas trop coûteux, mais cela sera très vite limité dès lors que l'on voudra gérer plusieurs sources lumineuse.

La technique à la mode de nos jours, démocratisée par Doom 3, utilise un rendu multi-passes. Cela permet de gérer correctement toutes les limitations de la méthode précédente, comme le montrent ces exemples :

A gauche : la technique à base de rectangle. A droite : le rendu multi-passes

Ce qui rend l'algorithme multi-passes exempt de bugs est le fait qu'il soit physiquement correct : en effet, au lieu d'assombrir une scène déjà éclairée, nous n'allons éclairer la scène que dans les zones non-ombrées. Ainsi une zone ombrée par une lumière n'aura pas la même intensité qu'une zone ombrée par plusieurs sources lumineuses (cf. premier exemple de l'image ci-dessus). Aussi, une zone non éclairée et une zone ombrée auront exactement la même couleur, (cf. second exemple).

Donc, concrètement, l'algorithme multi-passes, c'est quoi ? Le secret est, comme son nom l'indique, de rendre la scène plusieurs fois. Plus précisément, nous allons utiliser deux surfaces de rendu : une contenant la scène texturée non éclairée, et une autre contenant la somme des contributions des différentes sources lumineuses. Une passe finale modulera ces deux surfaces, produisant effectivement la scène correctement éclairée et ombrée.

Voici l'algorithme, avec le détail des états à activer et de la géometrie à rendre pour chaque passe :

//Passe 1 : scène texturée + Z-Buffer
  Activer l'écriture dans le color buffer
  Activer l'écriture dans le Z-Buffer
  Désactiver le stencil buffer
  Initialiser la fonction de comparaison Z à inférieur ou égal
  Afficher la scène texturée

//Passe 2 : contribution ambiante
  Utiliser la seconde surface de rendu (nous l'appelerons LightBuffer)
  Désactiver l'écriture dans le Z-Buffer
  Initialiser la fonction de comparaison Z à égal
  Désactiver les textures
  Afficher la scène avec uniquement la couleur ambiante des objets

//Passe 3 à N (1 passe par lumière) : ajout de la contribution des lumières
  Effacer le stencil buffer
  Afficher les volumes d'ombre générés par la lumière courante dans le stencil buffer
  Initialiser le test stencil pour n'autoriser que le rendu des pixels non ombrés
  Activer l'alpha-blending additif (one, one)
  Afficher la scène éclairée par la lumière courante

//Passe N + 1 : brouillard
  ...

//Passe finale : modulation de la scène texturée et de l'éclairage
  Utiliser la première surface de rendu (le back buffer)
  Placer LightBuffer comme texture
  Désactiver le stencil buffer
  Désactiver le test de Z
  Initialiser la fonction de comparaison Z à toujours
  Activer l'alpha-blending multiplicatif (destcolor, zero)
  Afficher un rectangle recouvrant tout l'écran

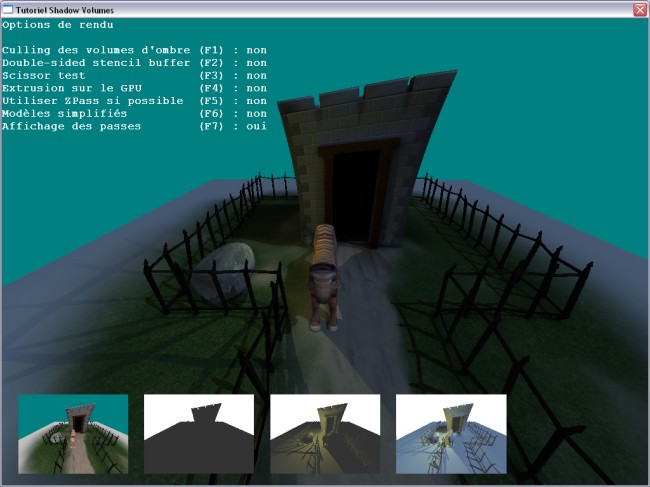
Voici la même chose en image (avec une seule lumière et pas de brouillard) :

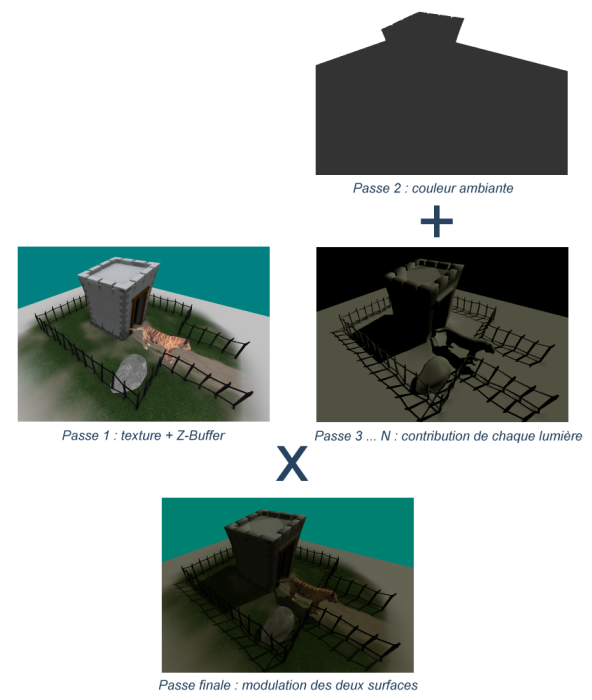Etapes de l'algorithme en images

Si certaines parties de l'algorithme ne vous parlent pas, vous pourrez trouver dans le code source joint à ce tutoriel un fichier effet DirectX qui est assez explicite quant aux changements d'états pour chaque passe.

Bien sûr si vous ne gérez pas la contribution ambiante ou encore le brouillard dans votre application, il sera inutile d'effectuer les passes correspondantes.

Tout cela peut sembler horriblement coûteux, mais ça ne l'est pas tant que ça : d'une part nous éliminons l'overdraw (affichage du même pixel plusieurs fois) puisque le Z-Buffer est rempli dès la première passe, et d'autre part le reste est assez léger puisque nous n'activons que très peu de choses à chaque passe.

A noter que ceci était une optimisation concernant la qualité de rendu, nous allons maintenant attaquer vraiment les optimisations de performances.

4. Utilisation intelligente du ZFail et du ZPass

Si vous avez bien suivi les tutoriels expliquant les bases des volumes d'ombre, il existe deux variantes de l'algorithme. Initialement existait le ZPass, très simple et performant, mais déraillant complétement lorsque la caméra se trouvait dans un volume d'ombre (ie. lorsque le plan de clipping proche coupait un volume). Aucune solution simple n'existant à ce problème, on a donc vu apparaître la seconde variante : le ZFail, démocratisé par John Carmack sous le nom de Carmack's reverse. Cela a éliminé le problème de clipping avec le plan proche, mais en a introduit un autre avec le plan lointain. Cependant on peut cette fois régler le problème, typiquement en "bouchant" le volume d'ombre de part et d'autre avec ce que l'on nomme le front cap et le back cap.
Le ZFail est donc plus compliqué à mettre en oeuvre, un poil moins performant, mais est plus robuste.

Cependant, étant donné que le ZPass ne pose problème que lorsque la caméra se trouve dans un volume d'ombre, ne pouvons-nous pas détecter cette situation et donc limiter l'utilisation du ZFail au strict minimum ? D'autant plus que dans la plupart des scènes ce genre de situation problématique n'arrivera que très rarement, et que nou pouvons réaliser ce test individuellement pour chaque objet. Au pire des cas vous rendrez donc peut-être un ou deux volumes d'ombres en ZFail, ce qui reste assez anecdotique.

Afin de détecter si la caméra se trouve dans un volume d'ombre ou non, la technique exacte serait de déterminer le volume formé par le plan de clipping proche et la source lumineuse (une pyramide donc) et de tester les intersections entre ce volume et tous les objets de la scène. Ceux qui coupent ce volume devront être rendus en ZFail, tous les autres pourront utiliser le ZPass.

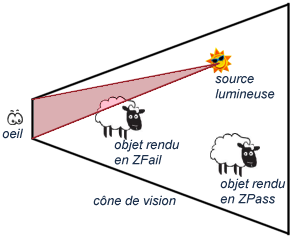Illustration de l'algorithme

Cependant, les tests d'intersection pyramide / objet ne sont ni les plus simples ni les moins coûteux, ainsi nous allons simplifier un peu le problème, quitte à perdre un peu en précision.

Premièrement nous allons utiliser une technique très commune lorsqu'il s'agit d'intersections : nous allons approximer les objets par leur volume englobant, en général par une sphère ou par une boîte. Nous détecterons potentiellement des intersections qui n'existent pas, mais peu importe, ce que nous allons gagner en complexité de calcul vaut largement la petite perte de précision engendrée.

Deuxièmement, nous allons réduire le plan de clipping proche à un unique point. Ainsi il suffira de tester un segment : celui qui relie la position de la caméra à la position de la source lumineuse (il faudra prendre un point infiniment éloigné pour le cas des lumières directionnelles). Ici la perte d'exactitude pourra par contre créer des petits artefacts, dans le cas très rare où seul un morceau du plan de clipping proche coupera un volume.
A vous de choisir donc : si ça reste négligeable dans votre application vous pourrez utiliser cette approximation, si par contre vous jugez que ce n'est pas acceptable alors libre à vous d'utiliser une pyramide et de mettre en place les algorithmes d'intersection appropriés.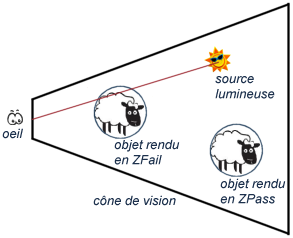

Algorithme simplifié à l'aide de formes plus basiques

Si vous choisissez la solution la plus simple, à savoir des tests segment / sphère, alors voici quelques détails.

5. Extruder à l'infini

Matrice, external triangles.

6. Extruder avec un vertex shader

7. Le double-sided stencil buffer

Le double-sided stencil buffer est une fonctionnalité qui a été "récemment" introduite dans toute bonne carte graphique, principalement pour le rendu de volumes d'ombre justement. Le principe est le suivant : plutôt que d'afficher les faces avant avec un certain parametrage du stencil buffer, puis les faces arrières avec d'autres paramètres, le double-sided stencil permet de combiner tout ça en un seul rendu ; les faces avant ET les faces arrières seront donc toutes tracées lors du même appel, et avec des paramètres de stencil bien différents. Attention à ne pas se leurrer cependant : le nombre de triangles traité ne sera pas plus faible, tout comme le nombre de pixels écrits. En fait si votre application est limitée par le fillrate (taux de remplissage des pixels) alors vous ne gagnerez même rien du tout. Dans le cas contraire vous pourrez par contre noter un gain léger, toujours appréciable surtout que pour tirer partie du double-sided stencil il suffit d'envoyer un ou deux flags à votre API 3D.

Afin de savoir si votre carte graphique supporte le double-sided stencil buffer, il faut vérifier la présence de l'extension GL_EXT_stencil_two_side sous OpenGL, ou du flag D3DSTENCILCAPS_TWOSIDED de D3DCAPS9.StencilCaps sous DirectX 9.

Algorithme ZFail sans double-sided stencil buffer :

// Parametrage des faces arrières
CullMode = Back
StencilZFailOp = Increment

// Rendu du volume d'ombre du modèle
Afficher(Volume)

// Parametrage des faces avant
CullMode = Front
StencilZFailOp = Decrement;

// Rendu du volume d'ombre du modèle
Afficher(Volume)

Algorithme ZFail avec double-sided stencil buffer :

// Il faut afficher les deux côtés
CullMode = FrontAndBack

// Parametrage des faces arrières
StencilZFailOpBack = Increment

// Parametrage des faces avant
StencilZFailOpFront = Decrement;

// Rendu du volume d'ombre du modèle
Afficher(Volume)

8. Le scissor test

9. Culling des volumes d'ombre

10. Utilisation de modèles simplifiés

Habituellement, les volumes d'ombre sont générés à partir des modèles affichés à l'écran. Une optimisation pourrait donc être tout simplement d'utiliser des modèles beaucoup moins détaillés. Etant donné que ces modèles ne sont utilisés que pour générer le volume d'ombre, la différence ne sera que très peu visible, voire quasiment invisible si vous vous débrouillez bien. On peut ainsi y aller franchement pour simplifier les modèles, et réduire le nombre de polygones utilisés par des facteurs de l'ordre de 5 à 20 selon les modèles.

Mais tout n'est pas si simple, et si les versions simplifiées de vos modèles ne satisfont pas une condition primordiale alors vous pourrez obtenir de drôles de résultats visuels. La condition à respecter est la suivante : le modèle simplifié doit être contenu entièrement dans le modèle original. Voici ce qui pourrait arriver si ce n'était pas le cas :

Artefact dû à l'utilisation d'une mesh simplifiée

A gauche : utilisation du modèle original. A droite : artefact produit par l'utilisation d'un modèle simplifié incorrect

Ainsi pour éviter les problèmes et avoir des modèles optimaux pour générer les volumes d'ombre, il vaudra mieux créer ceux-ci "à la main", ce qui permettra d'avoir un contrôle total. Bien sûr on ne peut pas toujours se payer ce luxe, et on pourra également coder un algorithme de simplification automatique. Attention à ne pas utiliser n'importe quel algorithme toutefois, il faut en choisir un qui satisfasse les conditions décrites ci-dessus.

11. Pour aller encore plus loin...

ZPass+ (citer les inconvénients et le blog de Lengyel) Silouhete tracking APIs nextgen et geometry buffers (Dx10)

12. Conclusion

Résultats en FPS de chaque optim ? Classement ?

13. Références

14. Téléchargements

Une petite démo interactive à été développée (en C++ avec DirectX) pour illustrer les techniques vues tout au long de ce tutoriel. Elle permet d'activer ou non les optimisations individuellement, ainsi que d'afficher les résultats intermédiaires des différentes passes.

Le package contient l'exécutable, les sources ainsi que les fichiers projet pour Visual C++ Express 2005.
Télécharger (zip, ... Mo)

Une version PDF de cet article est disponible : Télécharger (... Ko)

Si vous avez des suggestions, remarques, critiques, si vous avez remarqué une erreur, ou bien si vous souhaitez des informations complémentaires, n'hésitez pas à me contacter !

Note : quelques unes des images qui se trouvent sur cette page ne m'appartiennent pas et ont été trouvées un peu partout sur le web. Si l'utilisation de l'une d'entre elles pose le moindre souci, merci de me contacter.

Les sources présentées sur cette page sont libres de droits et vous pouvez les utiliser à votre convenance. Par contre, la page de présentation constitue une œuvre intellectuelle protégée par les droits d'auteur. Copyright © 2006 Laurent Gomila. Aucune reproduction, même partielle, ne peut être faite de ce site ni de l'ensemble de son contenu : textes, documents, images, etc. sans l'autorisation expresse de l'auteur. Sinon vous encourez selon la loi jusqu'à trois ans de prison et jusqu'à 300 000 € de dommages et intérêts.